题目:
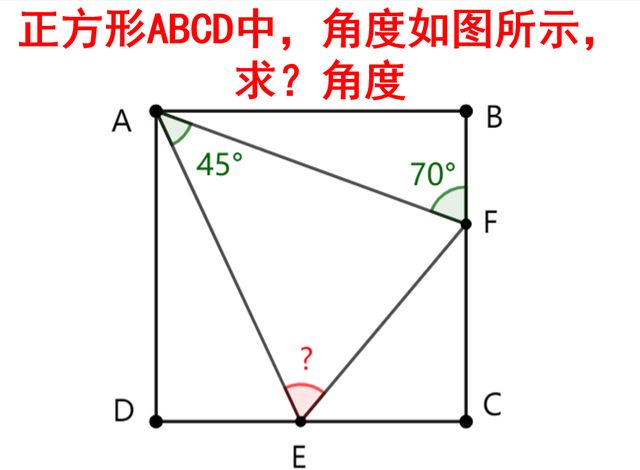
正方形ABCD中,角度如图所示,求?角度
知识点回顾:
正方形性质定理
两组对边分别平行;四条边都相等;邻边互相垂直。
四个角都是90°,内角和为360°。
对角线互相垂直;对角线相等且互相平分;每条对角线平分一组对角。
既是中心对称图形,又是轴对称图形(有四条对称轴)。
正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的夹角是45°;正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
正方形具有平行四边形、菱形、矩形的一切性质与特性。
正方形是特殊的矩形,正方形是特殊的菱形。
等腰直角三角形性质定理
两底角等于45°。
两腰相等。
等腰直角三角形三边比例为1:1:√2
等腰直角三角形判定定理
有一个角是直角的等腰三角形,或两条边相等的直角三角形是等腰直角三角形。
三边比例为1:1:√2的三角形是等腰直角三角形。
底角为45°的等腰三角形是等腰直角三角形。
有一个锐角是45°的直角三角形是等腰直角三角形。
直角边和斜边的比例为1:√2的直角三角形是等腰直角三角形。
有一个角是45°,并且这个角两边长度比为1:√2的三角形是等腰直角三角形。
全等三角形性质定理:
全等三角形的对应角相等。
全等三角形的对应边相等。
能够完全重合的顶点叫对应顶点。
全等三角形的对应边上的高对应相等。
全等三角形的对应角的角平分线相等。
全等三角形的对应边上的中线相等。
全等三角形面积和周长相等。
全等三角形的对应角的三角函数值相等。
全等三角形判定定理:
三边对应相等的三角形是全等三角形。
两边及其夹角对应相等的三角形是全等三角形。
两角及其夹边对应相等的三角形全等。
两角及其一角的对边对应相等的三角形全等。
在一对直角三角形中,斜边及另一条直角边相等。
三角相等,不能证全等,但能证相似三角形。
一角相等,且非夹角的两边相等。
粉丝解法1:
粉丝解法2:
粉丝解法3:
以A为顶点将△ADE逆时针旋转90*,将AD与AB边重合,则△AEF≌AD‘F,<AEF=<AD‘F=180*一45*一70*=65*。
粉丝解法4:
如图,把△ADE绕点A逆时针旋转90°,使AD与AB重合,E点旋转到E',由题意可知: ∠FAE'=∠FAB+∠EAD=90°-45°=45°=∠EAF,AE=AE',AF=AF,△AEF≌△AE'F,∠AFE=∠AFB=70°
∠AEF=180°—45°—70°=65°
粉丝解法5:
将△ABF顺时针旋转90度后,依两三角形全等可得所求角为:
180一45一70=65度